Quote:
Originally Posted by diabolical1
^ understood. 
but what i'm saying is the crank rotations are not relevant - at least, if they are, i don't see it.
for example, my manipulation of the 86 mm x 86 mm MR2 engine, simply yield roughly 499.5... cc per cylinder, which i then multiply by 4 and get 1998 cc. engine revolutions never figured into it. if this engine block were used with a 2-stroke or 4-stroke head, it's still 1998 total capacity.
the rotary does require 3 complete revolutions to fire all 6 faces, but i don't see how that affects total capacity, which is in fact 6 chambers, and it is the volume of those 6 chambers that yield it's total capacity/displacement.
it's just the way i see. |
The confusion with everyone is in how to view the rotors and what they are displacing in comparable fashion to a piston engine. Point-in-fact, you can not. As Rice has said it's a different cycle (though technically speaking, it's the same cycle as any other 4-stroke engine just with a different configuration--just look at the p-v diagrams).
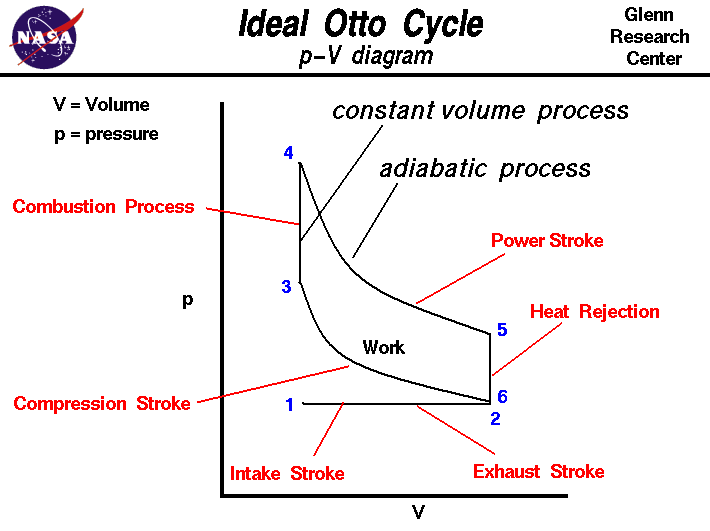http://www.grc.nasa.gov/WWW/k-12/airplane/otto.html
Each face sees that otto cycle after 3 revolutions of the crank shaft. There's no two ways about it. That's what each face sees. Thus the total displacement for all 6 faces comes out to the 4L or so that Rice posted up.
Now here's where I think everyone is getting messed up: As I posted previously each piston engine calculates displacement by going from tdc to bdc of each individual piston. Now lets compare this to the 13B. How many times do we have to turn the crank shaft to go from TDC to BDC for the front rotor housing (note I didn't say each individual face)? 1 right? 1 turn takes the front rotor from TDC to BDC, while the rear rotor is 180* out of phase (thus displacing the same amount). From which we have the standard nomenclature of 1.3L of displacement.
Does this make sense to everyone?
This method is scalable as well. To think of this clearly do not consider the rotor faces as pistons, but rather the rotor as a whole as equivalent to a piston (or think of the rotor housing as the piston equivalent sleeve). If the 20B were to be calculated using the method described above you would simply take the TDC to BDC of the front rotor (aka 1 revolution). Since all other rotors move the same amount with that 1 revolution they displace exactly the same amount of air. If you do not like that procedure simply take TDC to BDC of each rotor (they only take one revolution each) and it will displace the same amount of air. This is where the Mazda Displacement rating came from. This is the number you use (at least on the Haltech) when you put in the engines displacement. There's no black magic here.